TERCERA LEY
Tercera ley (1618): para cualquier planeta, el cuadrado de su período orbital es directamente proporcional al cubo de la longitud del semieje mayor de su órbita elíptica.
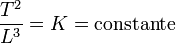
Donde, T es el periodo orbital (tiempo que tarda en dar una vuelta alrededor del Sol), (L) la distancia media del planeta con el Sol y K la constante de proporcionalidad.
Estas leyes se aplican a otros cuerpos astronómicos que se encuentran en mutua influencia gravitatoria, como el sistema formado por la Tierra y la Luna.
Tambien se dice que esta 3ra. ley de Kepler es una fórmula matemática. Significa que si usted sabe cuánto tiempo toma un planeta en circundar el Sol (p), después usted puede determinar a cuál distancia s e encuentra el planeta del Sol (a = eje semimayor de la órbita del planeta).
Esta fórmula también nos dice que los planetas lejanos del Sol tardan más tiempo en circundar al Sol que los que se encuentran cercanos al Sol. Se mueven más lentamente alrededor del Sol.
No dejes de ver la tabla de datos originales de los planetas . Notarás que el período orbital de los planetas (P) se hace más de largo a medida que va de Mercurio a Plutón.
